FAQ
Q1 : Quelle est la différence entre la microscopie numérique et optique ?
Le Hiscope HIROX est un microscope numérique, ce qui signifie que l'observation de l'échantillon ne se fait pas directement par la lentille mais au moyen d'une caméra qui capte l'image et la retransmet sur un écran.
Dès lors que ce choix de configuration a été fait, le système a été optimisé selon les caractéristiques du capteur - un rayon 2D plat avec une compatibilité aux taux de lecture, de taille d'affichage en pixels, de courbe de retour, etc.
Avec un microscope conventionnel, l'optique et la vue doivent être estimées et incluses dans les paramètres de configuration. Cette caractéristique peut éventuellement différer et fournir des résultats contradictoires lorsqu'on les compare avec les images obtenues depuis un microscope avec capteur numérique.
Puisque le HiScope a été conçu pour le numérique, aucun compromis n'a été fait afin de réaliser des ajustements selon les observations à l'oeil nu. Cependant, le système est en effet souvent capable de bénéficier de la vue humaine et du traitement des signaux visuels afin de fournir des résultats d'observation uniques, c.-à-d. la microscopie rotative 3D.
Q2 : Quels sont les avantages d'un microscope numérique ?
Nombre d'avantages du microscope numérique proviennent du fait que la sortie soit numérique.
Par exemple, puisque les images sont affichées sur un écran, tout le monde peut voir la même chose au même moment. Il n'est plus nécessaire d'essayer de décrire un petit défaut dans le coin supérieur gauche du champ de vision ou d'espérer que la prochaine personne qui observa l'échantillon ne verra pas simplement ses cils. L'image peut être immédiatement traitée, capturée, enregistrée, mesurée et corrigée.
Le traitement d'image peut non seulement améliorer la qualité de l'image mais aussi permettre l'agrandissement de la profondeur de champ (la quantité de profondeur dans l'image étant nette) en combinant l'information de netteté depuis plusieurs pans d'images.
Il y a d'autres avantages découlant directement de la configuration. Une des caractéristiques importantes de certaines lentilles est leur profondeur de champ inhabituellement grande. Cette dernière peut être plusieurs fois plus grande que celle d'un stéréomicroscope ou d'un microscope conventionnel même à grossissement similaire (souvent quelques millimètres au lieu de micromètres). On compte aussi parmi les avantages du microscope numérique les modes d'éclairage uniques et les possibilités d'observation sous des angles variés (le vue oblique dynamique n'étant pas possible avec un microscope conventionnel malgré les possibilités de vidéo).
Q3 : Qu'en est-il du grossissement ?
The short answer is NO, 300x in a digital microscope is not the same as 300x in a conventional microscope.
Just as the magnification of an image photographed in a conventional microscope depends on the size of the final print, so too the magnification of a digital microscope image will be determined by the size of the monitor on which it is displayed.
With digital microscopy it is really more relevant to talk about Field of View (FOV) rather than magnification – a 500-micrometer sample viewed on a 15″ computer display is much lower “mag” than the same sample viewed on a large screen with a video projector.
The question to ask is “What is the ratio of the size of the real object to its size in the digital image?” Generally, with a 15″ to 17″ monitor this works out to be roughly 40% to 60% of the magnification you would be accustomed to in a conventional microscope. That is, 1000x in a digital microscope would be approximately the same as 400x to 600x in a conventional microscope.
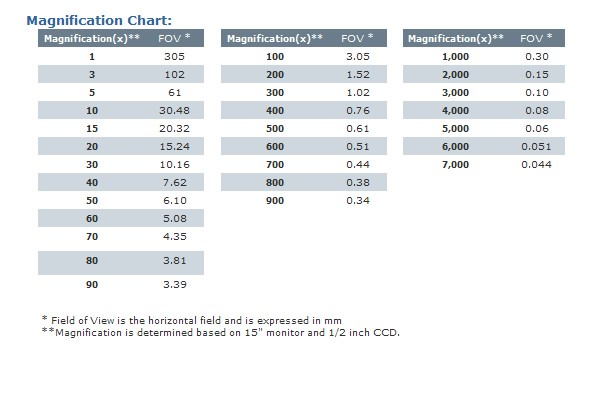
The HiScope nominal magnifications are given for display on a standard 15″ computer monitor. Table 1 gives a range of FOV for different magnifications.
Q4 : Quel champ de vision pour quel grossissement ?
Q5: Analog or Digital?
The choice of an analog video camera or digital one comes down to three main factors – display refresh rate, compatibility and cost.
Since microscopy is highly interactive, it is important to have the human interface to be as close to “realtime” as possible. “Realtime” has come to mean 25 to 30 frames per second (even motion pictures are 24 frame per second). The number is related to visual physiology – the critical flicker rate, the rate above which the image is perceived as being continuously presented.
Until quite recently, only true analog video cameras were capable of presenting data that quickly. NTSC analog video, when digitized is almost 30MB per second. Since the video standards are so widely accepted it is a simple matter to find compatible hardware a situation that does not yet exist in the digital image world where many imaging devices use interfaces that are far less common.
Except for the NTSC/PAL dichotomy, a video recording made on one machine is certain to play on any other comparable machine. Until quite recently, digital cameras with a resolution higher than analog video (640×480) that had a 30 frame per second output were quite expensive.
Our Hirox KH-1300/7700 units, however have overcome many of the limitation previously encountered in streaming digital imaging. With a standard UXGA (1600×1200) output, the camera can plug directly into a high resolution computer monitor.
What’s more, with new pixel shifting technology the field of view can be sub-pixel sampled to give images with 30 million pixels.
Even recording streaming digital signals is now a simple matter with the latest compression codecs.
Q6: What about system resolution?
Resolution in a digital microscope system can refer to several very different things. This is unfortunate because of the confusion the question of “what is the resolution?” brings.
First to consider: the resolution of the camera itself. This is sometimes expressed as some number of lines, i.e. 800 lines resolution, or given as the number of pixels in the camera array, i.e. 1600×1200. For line resolution the measurement is for the number of black and white line pairs that could be resolved if the central, highest resolution portion of the display were extended across the whole screen.
Pretty esoteric stuff since few people look at vertical black and white lines. The number is, though, a relative indication of how sharp the image will be – the higher the number the sharper the image that the camera is capable of producing. The case with high resolution digital cameras is almost straight forward since here all the pixels count- well most of them do anyway.
A camera with 1600×1200 sensor elements will make an image with 1600×1200 pixels. There is a little fudging because of the way the color is derived (demosaicing), but that is another, also somewhat complicated story. With the pixel shifted image however there is none of the demosaicing and each pixel really sees a red and blue and green signal – almost as if it were a 3 three chip camera.
Now to the microscope resolution part of the question:
Because the microscope has a zoom capability and can magnify an object to different sizes, the resolution will be dependent on both the magnification and the resolving power of the lens. The resolution of lenses is ultimately dependent on the wavelength of light – in air you simply cannot see anything below about half the wavelength of the illuminating light no matter how good the lens is or how much it will magnify.
Without getting too technical, the theoretical limit is about .33 micrometer laterally and about 1 micrometer vertically but the practical limit is usually a little higher, perhaps closer to 1 micrometer in the X/Y and 5 micrometers or more in the Z for lower magnification lenses.
In a perfect world, that would mean you need a minimum magnification of roughly 300x to be able to just resolve two 1-micrometer objects. In practical terms, samples rarely have the extreme contrast or other physical and optical properties necessary to allow that resolution at that magnification.
There is also the distinction that needs to be made between resolving, which is more of a theoretical exercise, and in being able to “see” the resolution. Sampling theory and optical physics define the resolving power of the system but, in practical terms, the magnification needs to be probably three to five times or more higher than theory would predict in order to have enough information in the image to actually “see” the resolution.
Higher magnification is indeed empty magnification but at least you will have the image spread across enough pixels to allow you to visually distinguish between adjacent objects.